关键词： 教师资格证

• *备考没方向？
• *考试时间不清楚？
• *成绩看不懂？
• *考试内容没有掌握？
• *拿证之后何去何从？
• *别人上岸也这么难？

扫码添加专属备考顾问
▪ 0元领取考点真题礼包
▪ 获取1对1备考指导

教学过程：

一、 课程导入

师：在几何问题的研究中，我们常常直接依据几何图形中点、线、面的关系研究几何图形的性质。现在我们采用另一种研究方法——坐标法来研究几何问题。坐标法是在坐标系的基础上，把几何问题转化为代数问题，通过代数运算研究几何图形性质的一种方法，这门科学称为解析几何。

师：我们都知道解析几何是17世纪法国数学家笛卡尔和费马共同创立的。解析几何的创立是数学发展史上的一个重要的里程碑，数学从此由常量数学进入变量数学时期。解析几何由此成为近代数学的基础之一。

师：本章我们主要研究的是直线与方程,这是我们在初中就熟悉的知识，当时是在函数的观点下进行的，是借助于“形”研究“数”的问题，从今天开始要转化一个角度，利用坐标系，借助于“数”研究“形”的问题，也就是用“坐标法”进行研究。这节课我们将研究最基础的知识--直线的倾斜角和斜率，在学习过程中体会和感受解析几何研究问题的基本方法和思想。

二、 新课讲解

师：老师这里有几个问题需要同学们帮老师解答一下，首先请你在平面直角坐标系中画出两条直线，并说出他们的不同之处。

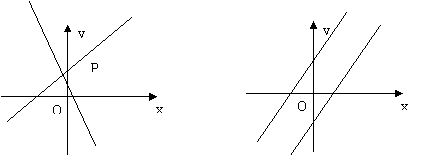
（1）                                    （2）

生：图(1)中的两条直线都经过点P , 但“倾斜程度”不同。图(2)中的两条直线“倾斜程度”相同，但没有公共点。

师：那么直线的倾斜程度是以什么为参照的？

生：以x轴或y轴为基准都可以，习惯上以x轴为基准。（教师引导）

师：在平面直角坐标系中，如何确定一条直线的位置？

生：（1）两点确定一条直线；   （2）一点及直线相对于x轴的“倾斜程度”。

师：两直线相交可以形成4个角，你愿意选择哪个角来描述直线的倾斜程度呢？

生：用图中的∠1。这个角就叫做直线的倾斜角。（教师引导）

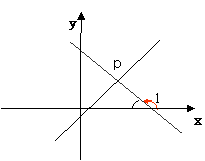
师：我们再来这个问题。在平面直角坐标系中，过一点的任意直线相对x轴的位置有哪些情形？请画出这些直线的倾斜角，并用你自己的语言说说倾斜角的三要素。

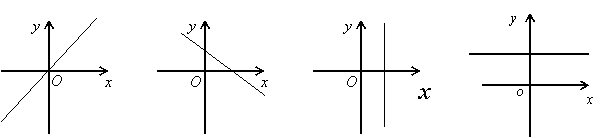
(１)                            (2)                                    (3)                                          (4)

师：根据同学们刚才的回答，我们可以得到倾斜角的定义：在直角坐标系下，以x轴为基准，当直线与轴相交时，轴正向与直线向上方向之间所成的角，叫做直线的倾斜角。规定：当直线与轴平行或重合时，它的倾斜角为0。

师：那么老师又有问题了，根据定义，倾斜角α的取值范围是什么呢?

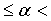生：0180。

师：我们继续思考：生活中，我们都有过爬山、爬坡的体验，你还知道表示倾斜程度的量吗？请举例。

生：可以用坡角与坡度来表示。

师：那么坡度的定义是什么？

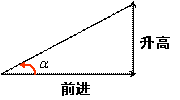
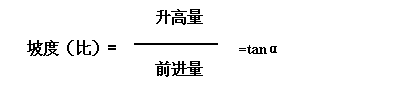
师：我们也可以用直线的倾斜角的正切来表示直线的倾斜程度即直线的斜率。斜率的定义：倾斜角不是90的直线，其倾斜角的正切值叫做这条直线的斜率。即。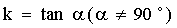

师：接下来，同学们完成下面的表格1，并分析直线的倾斜角不同时，直线的斜率取值是否也不同，在此基础上总结斜率的意义。

表1

师：除此之外，同学们根据三角函数的相关知识，思考当倾斜角α在[0，180）内变化时，斜率k如何变化？并填写表2。

表2

生：倾斜角α是90 o的直线没有斜率；倾斜角α不是90 o的直线都有斜率；倾斜角不同，直线的斜率也不同。斜率大于0的直线的倾斜角为锐角，并且斜率越大倾斜角越大；斜率小于0的直线的倾斜角为钝角，并且斜率越小倾斜角越大。因此，我们可以用斜率表示直线的倾斜程度。

师：我们已经学习过了坐标，那么如果已知直线将过两点P1（x1，y1），P2（x2，y2），试用点P1 、P2的坐标表示直线的斜率k？

生：经过两点P1（x1，y1），P2（x2，y2）（x1 x2）的直线的斜率公式是：。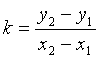

三、 巩固练习

师：下面我们看几道练习题。（教师指导学生回答）

例1.如图，已知A(3，2),B(-4，1),C（0，-1）,求直线AB，BC，CA的斜率，并判断这些直线的倾斜角是锐角还是钝角。

例2.在平面直角坐标系中，画出经过点（-1，2）且斜率分别为1，-1，和2的直线。

四、小结

师：请同学们谈谈你在这节课中学到哪些知识、思想方法和解决问题的经验？

生：1．明确了确定直线位置的几何要素。（两种）2．理解了刻画倾斜程度的量（倾斜角与斜率），知道了求斜率的两种方法（定义法、坐标法）。3．经历了用代数方法刻画斜率的过程,感受了数形结合与全面认识基础之上的分类讨论的数学思想。

五、作业

师：同学们回去之后想一想还有什么办法可以计算直线的斜率。

师：本节课是解析几何的第一课，“坐标法”是本课内容蕴含的核心思想方法，也是解析几何研究问题的核心思想方法，同学们要好好掌握。下课。

2024教资上岸大本营

• 考试公告
• 成绩查询
• 资格认定
• 备考讲座

扫码进群，备考路上不孤独，互帮互助，共同上岸！

点击打开